Introduction
GROOVE is a modelling and verification tool that will enable you to quickly and easily create graph transformation rules and apply them. Its strength lies in state space generation: once you have defined a start graph and a set of transformation rules, you can automatically apply the rules iteratively, generating all reachable graphs (or at least a finite number of them). This results in a (state) space of graphs, the analysis of which can help to establish correctness of the modelled system.
Beyond “simple” graphs and rules, GROOVE has some very powerful capabilities:
- Automatic isomorphism detection.
- Attribute manipulation.
- Nested graph conditions and transformation.
- Controlled rule application.
- Advanced state space exploration strategies.
- Model checking.
Runnable components
The GROOVE tool set has a number of runnable components:
-
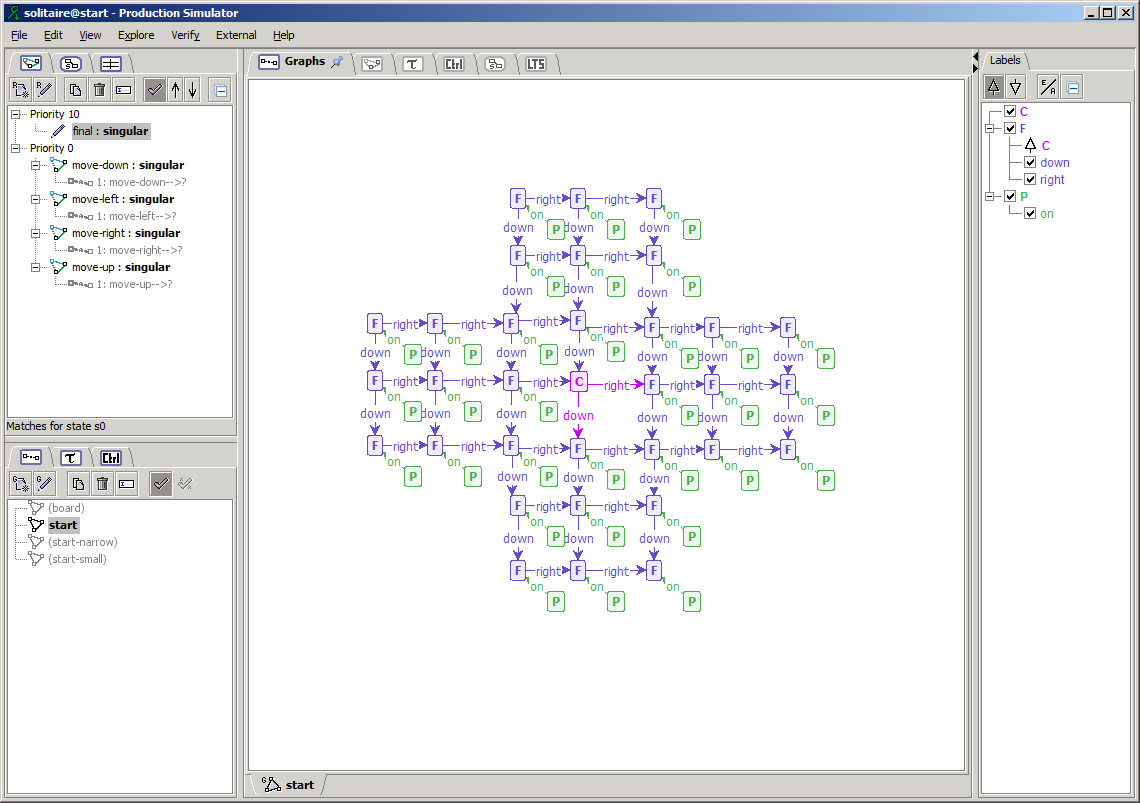
Simulator. A GUI that allows creation and graphical editing of Graph Transformation Systems (GTSs), and integrates the functionality of the Generator (see below). In addition, the Simulator allows the user to interactively explore the state space, by manually applying rules to a host graph.
-
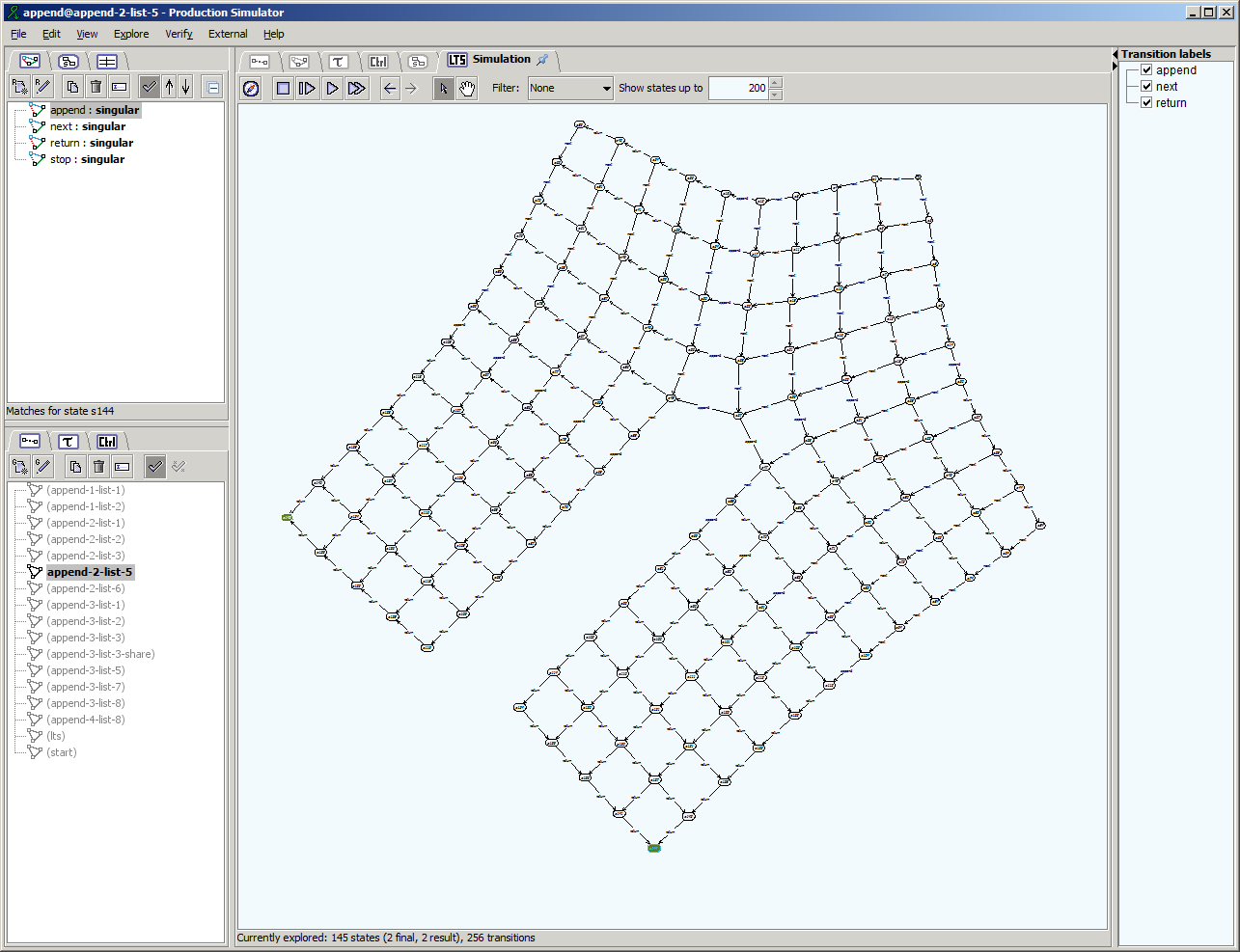
Generator. A command line tool that generates the state space of an existing GTS. The state space is stored as a Labelled Transition System (LTS), where each state is a graph and transitions are labelled by the rule applications. The strategy according to which the state space is explored (e.g., depth-first, breadth-first, etc) can be set as a parameter.
-
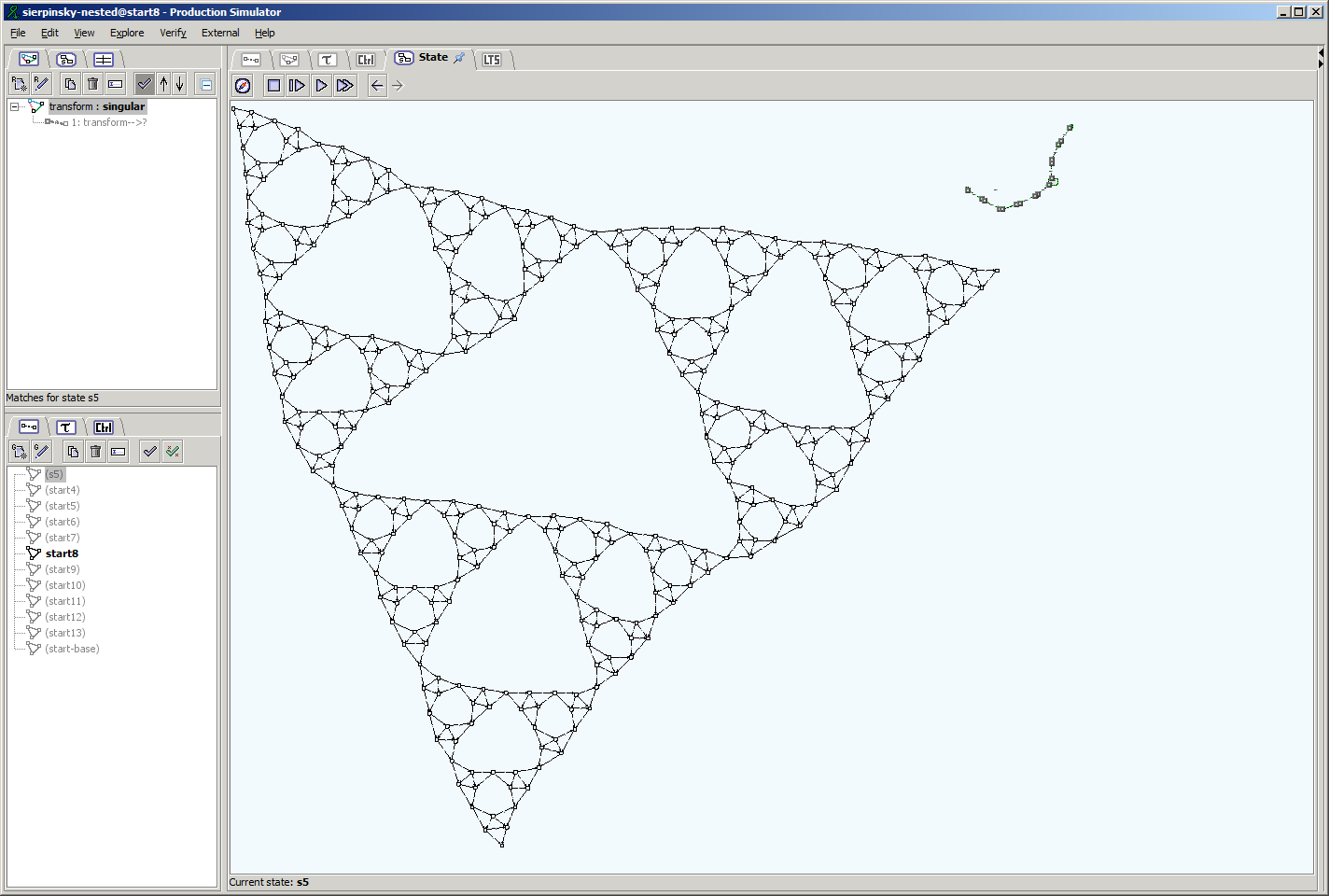
Viewer. A GUI that allows viewing of individual graphs (host graphs, rules or type graphs) outside the context of a GTS.
-
Imager. A tool that converts individual graphs (host graphs, rules or type graphs) to an image format such as JPG, GIF, SVG or PDF, which can in turn be included into other documents. The Imager can be invoked as a command-line tool or with a GUI.
Screenshots
Here are some screenshots of the Simulator, just to give you a first idea of the capabilities of GROOVE: